Vyřešeno 6 z 25 otázek.

VÝCHOZÍ TEXT K ÚLOZE 1

Matěj si na začátku srpna připravil částku, ze které po celý srpen platil všechny výdaje. Ve skutečnosti z ní utratil 15 % za jídlo, nájemné ho stálo o 200 % více než jídlo a za dopravu vydal o 60 % méně než za nájemné. Jiné výdaje Matěj v srpnu neměl, a zbytek připravené částky tedy uspořil.

(CZVV)

1 Vypočtěte, kolik procent částky připravené na srpen Matěj uspořil.

2 Pro $a,b,c \in R$ je dán vztah:

2a+ab^2+3c=0

Vyjádřete z tohoto vztahu neznámou $a$ .

Řešení úloha 2

Vyřešte pro: a (complex solution)

$\left\{\begin{matrix}a=-\frac{3c}{b^{2}+2}\text{, }&b\neq -\sqrt{2}i\text{ and }b\neq \sqrt{2}i\\a\in \mathrm{C}\text{, }&\left(b=\sqrt{2}i\text{ or }b=-\sqrt{2}i\right)\text{ and }c=0\end{matrix}\right.$

Postup řešení lineární rovnice

Odečtěte $3c$ od obou stran. Po odečtení hodnoty od nuly dostaneme stejnou zápornou hodnotu.

2a+ab^{2}=-3c

Slučte všechny členy obsahující $a$ .

\left(2+b^{2}\right)a=-3c

Slučte všechny členy obsahující proměnnou, jejíž hodnotu právě řešíte.

Rovnice je ve standardním tvaru.

\left(b^{2}+2\right)a=-3c

Vydělte obě strany hodnotou $2+b^{2}$ .

\frac{\left(b^{2}+2\right)a}{b^{2}+2}=-\frac{3c}{b^{2}+2}

Zrušte vynásobení vydělením obou stran stejným dělitelem.

Dělení číslem $2+b^{2}$ ruší násobení číslem $2+b^{2}$ .

a=-\frac{3c}{b^{2}+2}

Zrušte vynásobení.

3 Pro $x \in R \backslash \{0\}$ zjednodušte:

\left(\frac{\frac{x^2+10}{x}}{x}-1\right) \div \frac{5}{x}=

V záznamovém archu uveďte celý postup řešení.

Řešení úloha 3

Vyhodnotit

$\frac{2}{x}$

Stručný postup řešení

Vyjádřete $\frac{\frac{x^{2}+10}{x}}{x}$ jako jeden zlomek.

\frac{\frac{x^{2}+10}{xx}-1}{\frac{5}{x}}

Vynásobením $x$ a $x$ získáte $x^{2}$ .

\frac{\frac{x^{2}+10}{x^{2}}-1}{\frac{5}{x}}

Proveďte výpočet.

Pokud chcete sčítat nebo odčítat výrazy, rozšiřte je, aby měly stejné jmenovatele. Vynásobte číslo $1$ číslem $\frac{x^{2}}{x^{2}}$ .

\frac{\frac{x^{2}+10}{x^{2}}-\frac{x^{2}}{x^{2}}}{\frac{5}{x}}

Vzhledem k tomu, že $\frac{x^{2}+10}{x^{2}}$ a $\frac{x^{2}}{x^{2}}$ mají stejného jmenovatele, můžete je odečíst odečtením jejich čitatelů.

\frac{\frac{x^{2}+10-x^{2}}{x^{2}}}{\frac{5}{x}}

Slučte stejné členy ve výrazu $x^{2}+10-x^{2}$ .

\frac{\frac{10}{x^{2}}}{\frac{5}{x}}

Vydělte číslo $\frac{10}{x^{2}}$ zlomkem $\frac{5}{x}$ tak, že číslo $\frac{10}{x^{2}}$ vynásobíte převrácenou hodnotou zlomku $\frac{5}{x}$ .

\frac{10x}{x^{2}\times 5}

Vykraťte $5x$ v čitateli a jmenovateli.

\frac{2}{x}

4 V oboru R řešte:

\frac{x-2}{x^2+2x}+\frac{2x}{x+2}=1

V záznamovém archu uveďte celý postup řešení.

Řešení úloha 4

Vyřešte pro: x

$x=-1$ <br/> $x=2$

Postup použití rozkladu

Proměnná $x$ se nemůže rovnat žádné z těchto hodnot: $-2,0$ , protože není definováno dělení nulou. Vynásobte obě strany rovnice číslem $x\left(x+2\right)$ , nejmenším společným násobkem čísel $x^{2}+2x,x+2$ .

x-2+x\times 2x=x\left(x+2\right)

Vynásobením $x$ a $x$ získáte $x^{2}$ .

x-2+x^{2}\times 2=x\left(x+2\right)

Proveďte výpočet.

S využitím distributivnosti vynásobte číslo $x$ číslem $x+2$ .

x-2+x^{2}\times 2=x^{2}+2x

Proveďte roznásobení s využitím distributivnosti.

Odečtěte $x^{2}$ od obou stran.

x-2+x^{2}\times 2-x^{2}=2x

Sloučením $x^{2}\times 2$ a $-x^{2}$ získáte $x^{2}$ .

x-2+x^{2}=2x

Slučte stejné členy.

Odečtěte $2x$ od obou stran.

x-2+x^{2}-2x=0

Sloučením $x$ a $-2x$ získáte $-x$ .

-x-2+x^{2}=0

Slučte stejné členy.

Změňte uspořádání polynomu do standardního tvaru. Členy seřaďte od největší mocniny po nejmenší.

x^{2}-x-2=0

Chcete-li rovnici vyřešit, součinitel $x^{2}-x-2$ použijte vzorec $x^{2}+\left(a+b\right)x+ab=\left(x+a\right)\left(x+b\right)$ . Pokud chcete najít $a$ a $b$ , nastavte systém, který se má vyřešit.

a+b=-1

ab=-2

Vzhledem k tomu, že výraz $ab$ je záporný, mají hodnoty $a$ a $b$ opačné znaménko. Vzhledem k tomu, že výraz $a+b$ je záporný, má záporné číslo vyšší absolutní hodnotu než kladné číslo. Jediná taková dvojice představuje systémové řešení.

a=-2

b=1

Přepište rozložený výraz $\left(x+a\right)\left(x+b\right)$ pomocí získaných hodnot.

\left(x-2\right)\left(x+1\right)

Chcete-li najít řešení rovnic, vyřešte $x-2=0$ a $x+1=0$ .

x=2

x=-1

Postup použití rozkladu vytýkáním

x-2+x\times 2x=x\left(x+2\right)

Vynásobením $x$ a $x$ získáte $x^{2}$ .

x-2+x^{2}\times 2=x\left(x+2\right)

Proveďte výpočet.

S využitím distributivnosti vynásobte číslo $x$ číslem $x+2$ .

x-2+x^{2}\times 2=x^{2}+2x

Proveďte roznásobení s využitím distributivnosti.

Odečtěte $x^{2}$ od obou stran.

x-2+x^{2}\times 2-x^{2}=2x

Sloučením $x^{2}\times 2$ a $-x^{2}$ získáte $x^{2}$ .

x-2+x^{2}=2x

Slučte stejné členy.

Odečtěte $2x$ od obou stran.

x-2+x^{2}-2x=0

Sloučením $x$ a $-2x$ získáte $-x$ .

-x-2+x^{2}=0

Slučte stejné členy.

Změňte uspořádání polynomu do standardního tvaru. Členy seřaďte od největší mocniny po nejmenší.

x^{2}-x-2=0

Chcete-li rovnici vyřešit, koeficient na levé straně seskupte. Nejprve je třeba přepsát levou stranu jako $x^{2}+ax+bx-2$ . Pokud chcete najít $a$ a $b$ , nastavte systém, který se má vyřešit.

a+b=-1

ab=1\left(-2\right)=-2

a=-2

b=1

Zapište $x^{2}-x-2$ jako: $\left(x^{2}-2x\right)+\left(x-2\right)$ .

\left(x^{2}-2x\right)+\left(x-2\right)

Vytkněte $x$ z výrazu $x^{2}-2x$ .

x\left(x-2\right)+x-2

Vytkněte společný člen $x-2$ s využitím distributivnosti.

\left(x-2\right)\left(x+1\right)

Chcete-li najít řešení rovnic, vyřešte $x-2=0$ a $x+1=0$ .

x=2

x=-1

Postup použití kvadratické rovnice

x-2+x\times 2x=x\left(x+2\right)

Vynásobením $x$ a $x$ získáte $x^{2}$ .

x-2+x^{2}\times 2=x\left(x+2\right)

Proveďte výpočet.

S využitím distributivnosti vynásobte číslo $x$ číslem $x+2$ .

x-2+x^{2}\times 2=x^{2}+2x

Proveďte roznásobení s využitím distributivnosti.

Odečtěte $x^{2}$ od obou stran.

x-2+x^{2}\times 2-x^{2}=2x

Sloučením $x^{2}\times 2$ a $-x^{2}$ získáte $x^{2}$ .

x-2+x^{2}=2x

Slučte stejné členy.

Odečtěte $2x$ od obou stran.

x-2+x^{2}-2x=0

Sloučením $x$ a $-2x$ získáte $-x$ .

-x-2+x^{2}=0

Slučte stejné členy.

Všechny rovnice ve tvaru $ax^{2}+bx+c=0$ je možné vyřešit jako kvadratickou rovnici: $\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$ . Výsledkem kvadratické rovnice jsou dvě řešení, jedno pro součet a druhé pro rozdíl $\pm$ .

x^{2}-x-2=0

Tato rovnice má standardní tvar: $ax^{2}+bx+c=0$ . Do kvadratického vzorce, $\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$ , dosaďte $1$ za $a$ , $-1$ za $b$ a $-2$ za $c$ .

x=\frac{-\left(-1\right)\pm\sqrt{1-4\left(-2\right)}}{2}

Vynásobte číslo $-4$ číslem $-2$ .

x=\frac{-\left(-1\right)\pm\sqrt{1+8}}{2}

Přidejte uživatele $1$ do skupiny $8$ .

x=\frac{-\left(-1\right)\pm\sqrt{9}}{2}

Vypočítejte druhou odmocninu čísla $9$ .

x=\frac{-\left(-1\right)\pm3}{2}

Opakem $-1$ je $1$ .

x=\frac{1\pm3}{2}

Teď vyřešte rovnici $x=\frac{1\pm3}{2}$ , když $\pm$ je plus. Přidejte uživatele $1$ do skupiny $3$ .

x=\frac{4}{2}

Vydělte číslo $4$ číslem $2$ .

x=2

Teď vyřešte rovnici $x=\frac{1\pm3}{2}$ , když $\pm$ je minus. Odečtěte číslo $3$ od čísla $1$ .

x=-\frac{2}{2}

Vydělte číslo $-2$ číslem $2$ .

x=-1

Rovnice je teď vyřešená.

x=2

x=-1

Postup doplnění na druhou mocninu dvojčlenu

x-2+x\times 2x=x\left(x+2\right)

Vynásobením $x$ a $x$ získáte $x^{2}$ .

x-2+x^{2}\times 2=x\left(x+2\right)

Proveďte výpočet.

S využitím distributivnosti vynásobte číslo $x$ číslem $x+2$ .

x-2+x^{2}\times 2=x^{2}+2x

Proveďte roznásobení s využitím distributivnosti.

Odečtěte $x^{2}$ od obou stran.

x-2+x^{2}\times 2-x^{2}=2x

Sloučením $x^{2}\times 2$ a $-x^{2}$ získáte $x^{2}$ .

x-2+x^{2}=2x

Slučte stejné členy.

Odečtěte $2x$ od obou stran.

x-2+x^{2}-2x=0

Sloučením $x$ a $-2x$ získáte $-x$ .

-x-2+x^{2}=0

Slučte stejné členy.

Přidat $2$ na obě strany. Po přičtení hodnoty nula dostaneme původní hodnotu.

-x+x^{2}=2

Takové kvadratické rovnice je možné vyřešit doplněním na druhou mocninu dvojčlenu. Pokud chcete rovnici doplnit na druhou mocninu dvojčlenu, musí být nejdříve ve tvaru $x^{2}+bx=c$ .

x^{2}-x=2

Vydělte $-1$ , koeficient $x$ termínu $2$ k získání $-\frac{1}{2}$ . Potom přidejte čtvereček $-\frac{1}{2}$ na obě strany rovnice. Tímto krokem bude levá strana rovnice ve výrazu o dokonalý čtverec.

x^{2}-x+\left(-\frac{1}{2}\right)^{2}=2+\left(-\frac{1}{2}\right)^{2}

Umocněte zlomek $-\frac{1}{2}$ na druhou tak, že umocníte na druhou čitatele i jmenovatele zlomku.

x^{2}-x+\frac{1}{4}=2+\frac{1}{4}

Přidejte uživatele $2$ do skupiny $\frac{1}{4}$ .

x^{2}-x+\frac{1}{4}=\frac{9}{4}

Činitel $x^{2}-x+\frac{1}{4}$ . Obecně platí, že pokud je $x^{2}+bx+c$dokonalý čtverec, dá se vždy rozložit jako $\left(x+\frac{b}{2}\right)^{2}$ .

\left(x-\frac{1}{2}\right)^{2}=\frac{9}{4}

Vypočítejte druhou odmocninu obou stran rovnice.

\sqrt{\left(x-\frac{1}{2}\right)^{2}}=\sqrt{\frac{9}{4}}

Proveďte zjednodušení.

x-\frac{1}{2}=\frac{3}{2}

x-\frac{1}{2}=-\frac{3}{2}

Připočítejte $\frac{1}{2}$ k oběma stranám rovnice.

x=2

x=-1

5

5.1 Pro $n \in N$ upravte na mocninu o základu 64:

8 \cdot 64^n=

5.2 Pro $n \in N$ vyjádřete výrazem ve tvaru jediné mocniny:

20 % z $25^2$

Řešení úloha 5.1

Vyhodnotit

$8\times 64^{n}$

6 Předpis funkce $f$ definované pro všechna přípustná $x \in R$ je:

y = log_{10}(8-2x) - log_{10}(2-x)

Určete všechna $x \in R$ , pro která je hodnota funkce $f$ rovna 1. V záznamovém archu uveďte celý postup řešení.

Řešení úloha 6

Error

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 7

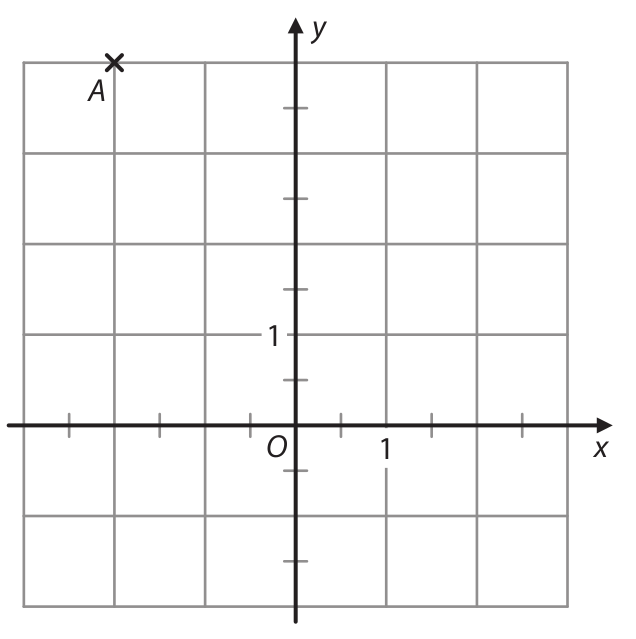
Funkce $g: y=a^x$ se základem $a \in R^+ \backslash \{1\}$ je definována pro všechna $x \in R$ . Její graf prochází bodem A[−2;4].

$alt text$

(CZVV)

7

7.1 Zapište souřadnici $b_2$ bodu B[2; $b_2$ ] grafu funkce $g$ .

7.2 V kartézské soustavě souřadnic Oxy sestrojte graf funkce $𝑔$ .

V záznamovém archu obtáhněte vše propisovací tužkou.

8

Funkce $h:y=-(x+6)^{2}+4$ s definičním oborem R je v jednom ze dvou intervalů (−∞;p⟩, ⟨p;+∞) klesající a ve zbývajícím je rostoucí ( $p \in R$ ).

Z obou intervalů vyberte ten, v němž je funkce $h$ rostoucí, a zapište jej s konkrétním číslem $p$ .

9 V rostoucí aritmetické posloupnosti $(a_n)_{n=1}^\infty$ je pátý člen $a_5=0$ .

Vypočtěte, kolikrát je dvacátý člen $a_{20}$ větší než desátý $a_{10}$ .

VÝCHOZÍ TEXT K ÚLOZE 10

Na 100 km jízdy spotřeboval automobil A 7 litrů benzinu a automobil B o $x$ litrů benzinu méně než automobil A.

Cena benzinu byla 40 Kč za litr.

(CZVV)

10

10.1 Vypočtěte v Kč průměrné výdaje za benzin na 1 kilometr jízdy automobilu A.

Výsledek nezaokrouhlujte.

10.2 V závislosti na $x$ vyjádřete v Kč průměrné výdaje za benzin na 1 kilometr jízdy automobilu B.

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOHÁM 11–12

V kartézské soustavě souřadnic Oxy jsou umístěny rovnoběžné přímky p, q.
Přímka p protíná souřadnicové osy v mřížových bodech A, B.
Přímka q prochází bodem Q[−6;4].

$alt text$

(CZVV)

11 V parametrickém vyjádření přímky p doplňte pravou stranu první rovnice.

\begin{aligned} p:&x = \qquad\quad,\\ &y = 0 + 5t, t \in R \end{aligned}

Řešení úloha 11

Error

12 Zapište obě souřadnice průsečíku D přímky q se souřadnicovou osou y.

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 13

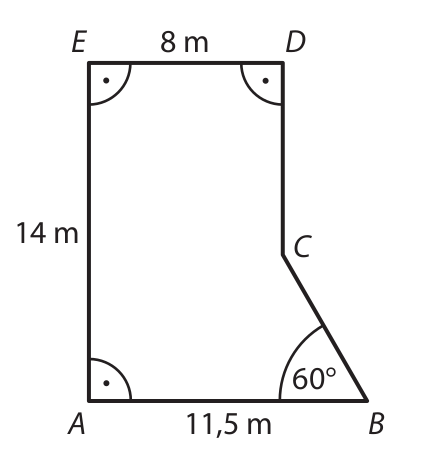
Stavba má tvar pětibokého kolmého hranolu s výškou 5 metrů. Na obrázku je zakreslena podstava ABCDE tohoto hranolu.

$alt text$

(CZVV)

13 Vypočtěte

13.1 v m² obsah boční stěny hranolu, která obsahuje podstavnou hranu BC,

13.2 v m³ objem hranolu.

Výsledky zaokrouhlete na celá čísla, dílčí výpočty nezaokrouhlujte. V záznamovém archu uveďte v obou částech úlohy celý postup řešení.

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 14

Čtvercový pozemek má stejnou výměru (obsah) jako obdélníkový pozemek.

Obdélníkový pozemek má jednu stranu o 35 % kratší než čtvercový pozemek a druhou stranu o 140 metrů delší než čtvercový pozemek.

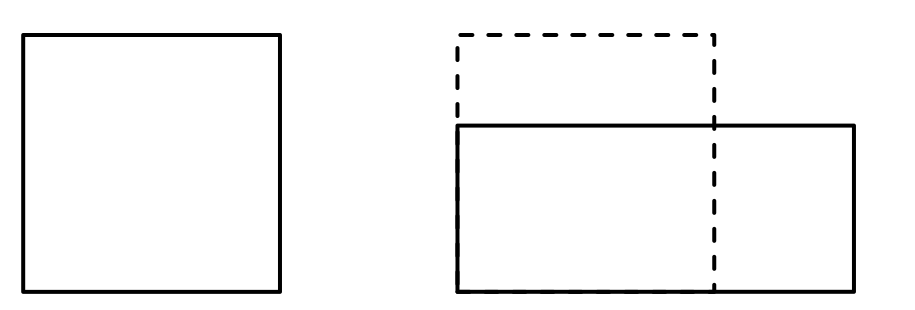
$alt text$

(CZVV)

14 Užitím rovnice nebo soustavy rovnic vypočtěte v metrech obvod čtvercového pozemku.

V záznamovém archu uveďte celý postup řešení (popis neznámých, sestavení rovnice, resp. soustavy rovnic, řešení a odpověď ).

15 Rozhodněte o každém z následujících tvrzení (15.1–15.3), zda je pravdivé (A), či nikoli (N).

15.1 Nerovnice $(x-3)(3-x)\geq0$ má v oboru R více než jedno řešení.

15.2 Řešením nerovnice $(x+4)(x+4)\geq0$ v oboru R je každé reálné číslo.

15.3 Množinou všech řešení nerovnice $\frac{x-2}{2-x}>0$ v oboru R je prázdná množina.

16 Vektor $\vec{u}=(3;\vec{u}_{2})$ je kolmý k vektoru $\vec{w}=(-3;1)$ .

Jaká je velikost vektoru $\vec{u}$ ?

[A] $3\sqrt{10}$
[B] $\sqrt{10}$
[C] 10
[D] 3
[E] jiná velikost

VÝCHOZÍ TEXT K ÚLOZE 17

Všechny čtyři vrcholy kosočtverce ABCD leží na souřadnicových osách kartézské soustavy souřadnic Oxy. Pro vrcholy A, B kosočtverce platí, že orientovaná úsečka AB je umístěním vektoru $\vec{v}$ =(12;5).

(CZVV)

17 Jaký je obsah kosočtverce ABCD?

[A] 52
[B] 60
[C] 120
[D] 169
[E] jiný obsah

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 18

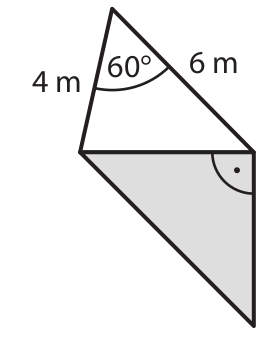
Nad pískovištěm je natažena stínicí plachta tvaru čtyřúhelníku,
který se skládá ze dvou trojúhelníků – bílého a šedého. Šedý trojúhelník je rovnoramenný a pravoúhlý.

$alt text$

(CZVV)

18 Jaký je obsah šedého trojúhelníku?

[A] 10,0 m²
[B] 10,4 m²
[C] 13,0 m²
[D] 13,5 m²
[E] 14,0 m²

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 19

Papírový klobouk se skládá ze tří částí – střechy, koruny a krempy.

Střechu tvoří kruh, který je horní podstavou rotačního válce.

Koruna je pláštěm tohoto válce a jejím rozvinutím
by vznikl obdélník o rozměrech 60 cm a 30 cm,
druhý rozměr je výškou válce.

Krempa má tvar mezikruží o šířce 5 cm.

Klobouk byl vyroben z papíru, který je
z jedné strany modrý a z druhé bílý.

Jednotlivé části klobouku k sobě
přiléhají svými okraji a jsou sešity nití.

$alt text$

(CZVV)

19 Jaký je obsah všech modrých ploch klobouku?

Výsledek je zaokrouhlen na celé cm².

[A] 2 086 cm²
[B] 2 465 cm²
[C] 4 472 cm²
[D] 4 851 cm²
[E] jiný obsah

VÝCHOZÍ TEXT K ÚLOZE 20

Předpis funkce $h$ definované pro všechna $x \in R$ je:

$y=2-x$

(CZVV)

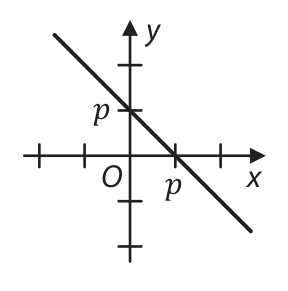
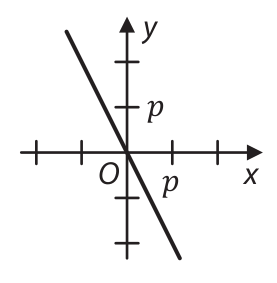
20 Který z následujících grafů je pro vhodné kladné číslo 𝑝𝑝 grafem funkce ℎ v kartézské soustavě souřadnic Oxy?

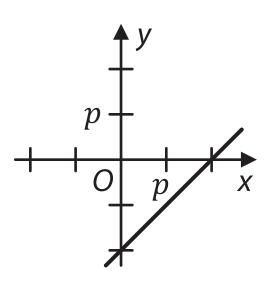
[A] $alt text$
[B] $alt text$
[C] $alt text$
[D] $alt text$
[E] $alt text$

VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 21

Mozaika je tvořena řadami stejných ornamentů.

První řada mozaiky obsahuje 3 ornamenty.
Každá další řada obsahuje o 2 ornamenty více než předchozí řada.

Poslední řada mozaiky obsahuje 99krát více ornamentů než první řada.

$alt text$

(CZVV)

21 Kolik ornamentů obsahuje celá mozaika?

[A] 15 000
[B] 22 200
[C] 29 700
[D] 30 000
[E] jiný počet

VÝCHOZÍ TEXT K ÚLOZE 22

První dva členy aritmetické posloupnosti jsou zároveň prvními dvěma členy geometrické posloupnosti. Přitom první člen je o 8 menší než druhý a druhý člen je pětkrát větší než první.

(CZVV)

22 Kolikátý člen aritmetické posloupnosti je roven třetímu členu geometrické posloupnosti?

[A] žádný člen
[B] pátý člen
[C] šestý člen
[D] sedmý člen
[E] osmý člen

VÝCHOZÍ TEXT K ÚLOZE 23

Ve městě se postupně ruší poštovní schránky a nové se nezřizují.

Počet poštovních schránek na konci každého kalendářního roku je vždy nižší alespoň o 12 %, ale nejvýše o 14 % počtu poštovních schránek, které byly ve městě na počátku téhož roku.

Na konci roku 2021 (tj. na počátku roku 2022) bylo ve městě 38 poštovních schránek.

(CZVV)

23 Kolik poštovních schránek se ve městě zrušilo během dvouletého období 2021 až 2022?

[A] Nelze jednoznačně určit.
[B] právě 9
[C] právě 10
[D] právě 11
[E] právě 12

VÝCHOZÍ TEXT A TABULKA K ÚLOZE 24

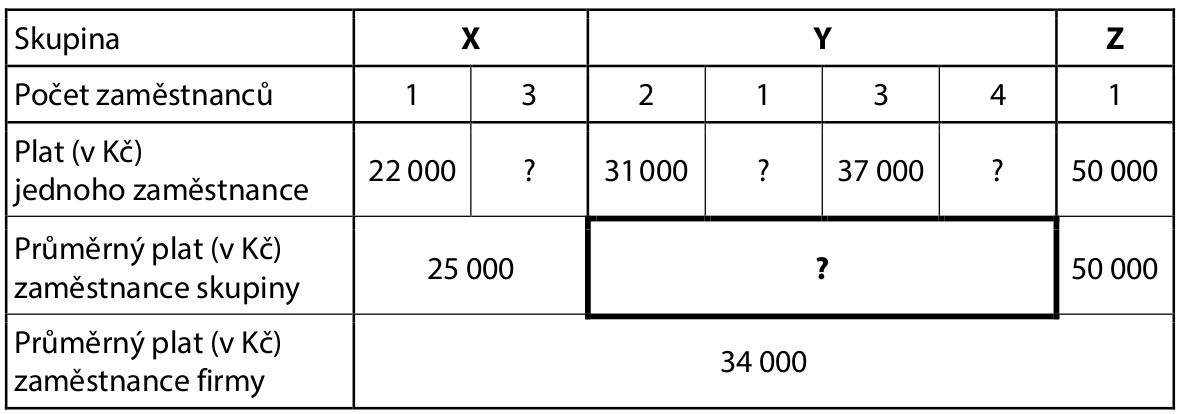
Všech 15 zaměstnanců firmy je rozděleno do tří různě početných skupin.
V tabulce jsou uvedeny některé údaje o platech těchto zaměstnanců.

$|Skupina|X|X|Y|Y|Y|Y|Z| |-------|:---:|:---:|:---:|:---:|:---:|:---:|:---:| |Počet zaměstnanců |1 |3 |2 |1 |3 |4 |1 | |Plat (v Kč)jednoho zaměstnance |22 000 |? |31 000 |? |37 000 |? |50 000 | |Průměrný plat (v Kč) zaměstnance skupiny|25 000 |25 000 |?|?|?|?|50 000 | |Průměrný plat (v Kč) zaměstnance firmy |34 000 |34 000 |34 000 |34 000 |34 000 |34 000 |34 000 |$

(CZVV)

24 Jaký je průměrný plat zaměstnance skupiny Y?

[A] nižší než 27 000 Kč
[B] 27 000 Kč
[C] 36 000 Kč
[D] vyšší než 36 000 Kč
[E] Nelze jednoznačně určit.

VÝCHOZÍ TEXT A TABULKA K ÚLOZE 25

V osudí je deset stejných míčků, každý je označen jedním z písmen A, B, C.
Tabulka udává rozdělení četností písmen.

Písmeno A B C

Četnost 5 2 3

Z osudí postupně po jednom vylosujeme 3 míčky, které do osudí nevracíme.
Jejich písmena zapíšeme zleva doprava v pořadí, v jakém byly míčky vylosovány.

(CZVV)


Písmeno	A	B	C
Četnost	5	2	3

25 Ke každému jevu (25.1–25.2) přiřaďte pravděpodobnost (A–F), s níž jev nastane.

25.1 Zápis písmen vylosovaných míčků je ABC.

25.2 Zápis písmen vylosovaných míčků je BCC.

[A] $\frac{1}{4}$
[B] $\frac{1}{12}$
[C] $\frac{1}{20}$
[D] $\frac{1}{24}$
[E] $\frac{1}{60}$
[F] jiná hodnota pravděpodobnosti

1 Vypočtěte, kolik procent částky připravené na srpen Matěj uspořil.

2 Pro a,b,c∈Ra,b,c \in Ra,b,c∈R je dán vztah:

Vyřešte pro: a (complex solution)

3 Pro x∈R\{0}x \in R \backslash \{0\}x∈R\{0} zjednodušte:

Vyhodnotit

4 V oboru R řešte:

Vyřešte pro: x

5

5.1 Pro n∈Nn \in Nn∈N upravte na mocninu o základu 64:

5.2 Pro n∈Nn \in Nn∈N vyjádřete výrazem ve tvaru jediné mocniny:

Vyhodnotit

6 Předpis funkce fff definované pro všechna přípustná x∈Rx \in Rx∈R je:

Error

7

7.1 Zapište souřadnici b2b_2b2​ bodu B[2;b2b_2b2​] grafu funkce ggg.

7.2 V kartézské soustavě souřadnic Oxy sestrojte graf funkce 𝑔𝑔g.

8

9 V rostoucí aritmetické posloupnosti (an)n=1∞(a_n)_{n=1}^\infty(an​)n=1∞​ je pátý člen a5=0a_5=0a5​=0.

10

10.1 Vypočtěte v Kč průměrné výdaje za benzin na 1 kilometr jízdy automobilu A.

10.2 V závislosti na xxx vyjádřete v Kč průměrné výdaje za benzin na 1 kilometr jízdy automobilu B.

11 V parametrickém vyjádření přímky p doplňte pravou stranu první rovnice.

Error

12 Zapište obě souřadnice průsečíku D přímky q se souřadnicovou osou y.

13 Vypočtěte

13.1 v m2 obsah boční stěny hranolu, která obsahuje podstavnou hranu BC,

13.2 v m3 objem hranolu.

14 Užitím rovnice nebo soustavy rovnic vypočtěte v metrech obvod čtvercového pozemku.

15 Rozhodněte o každém z následujících tvrzení (15.1–15.3), zda je pravdivé (A), či nikoli (N).

15.1 Nerovnice (x−3)(3−x)≥0(x-3)(3-x)\geq0(x−3)(3−x)≥0 má v oboru R více než jedno řešení.

15.2 Řešením nerovnice (x+4)(x+4)≥0(x+4)(x+4)\geq0(x+4)(x+4)≥0 v oboru R je každé reálné číslo.

15.3 Množinou všech řešení nerovnice x−22−x>0\frac{x-2}{2-x}>02−xx−2​>0 v oboru R je prázdná množina.

16 Vektor u⃗=(3;u⃗2)\vec{u}=(3;\vec{u}_{2})u=(3;u2​) je kolmý k vektoru w⃗=(−3;1)\vec{w}=(-3;1)w=(−3;1).

17 Jaký je obsah kosočtverce ABCD?

18 Jaký je obsah šedého trojúhelníku?

19 Jaký je obsah všech modrých ploch klobouku?

20 Který z následujících grafů je pro vhodné kladné číslo 𝑝𝑝 grafem funkce ℎ v kartézské soustavě souřadnic Oxy?

21 Kolik ornamentů obsahuje celá mozaika?

22 Kolikátý člen aritmetické posloupnosti je roven třetímu členu geometrické posloupnosti?

23 Kolik poštovních schránek se ve městě zrušilo během dvouletého období 2021 až 2022?

24 Jaký je průměrný plat zaměstnance skupiny Y?

25 Ke každému jevu (25.1–25.2) přiřaďte pravděpodobnost (A–F), s níž jev nastane.

25.1 Zápis písmen vylosovaných míčků je ABC.

25.2 Zápis písmen vylosovaných míčků je BCC.

2 Pro $a,b,c \in R$ je dán vztah:

3 Pro $x \in R \backslash \{0\}$ zjednodušte:

5.1 Pro $n \in N$ upravte na mocninu o základu 64:

5.2 Pro $n \in N$ vyjádřete výrazem ve tvaru jediné mocniny:

6 Předpis funkce $f$ definované pro všechna přípustná $x \in R$ je:

7.1 Zapište souřadnici $b_2$ bodu B[2; $b_2$ ] grafu funkce $g$ .

7.2 V kartézské soustavě souřadnic Oxy sestrojte graf funkce $𝑔$ .

9 V rostoucí aritmetické posloupnosti $(a_n)_{n=1}^\infty$ je pátý člen $a_5=0$ .

10.2 V závislosti na $x$ vyjádřete v Kč průměrné výdaje za benzin na 1 kilometr jízdy automobilu B.

13.1 v m² obsah boční stěny hranolu, která obsahuje podstavnou hranu BC,

13.2 v m³ objem hranolu.

15.1 Nerovnice $(x-3)(3-x)\geq0$ má v oboru R více než jedno řešení.

15.2 Řešením nerovnice $(x+4)(x+4)\geq0$ v oboru R je každé reálné číslo.

15.3 Množinou všech řešení nerovnice $\frac{x-2}{2-x}>0$ v oboru R je prázdná množina.

16 Vektor $\vec{u}=(3;\vec{u}_{2})$ je kolmý k vektoru $\vec{w}=(-3;1)$ .